T-QAD Day 14 @ 30 April 2020

Notes Topic: Functions

Subtopic: Inverse functions

T-QAD for Today

Question 1 : Q1/D14/300420

Given the functions f(x) = 4 - 5x and g(x)=x²-2, find
(a) f ^-1(x)

(b) the value of f ^-1g(4)

                                                                                    (5 marks)

Question 2 : Q2/D14/300420

Write down the values of :

(a) f ^-1(-5)

(b) gf (-2)

                                                                                    (2 marks)

Answers T-QAD 29 April 2020

Check your answer and fill in the form to record your marks.

MyMarks 

Question 1:

Question 2 (a):

Question 2 (b):

T-QAD Day 13 @ 29 April 2020

Notes Topic: Functions

Subtopic: Composite functions

 T-QAD for TODAY

Question 1 : Q1/D13/290420

Given the functions f(x) = p - 2x and g(x) = 3x² – 7  

find the value of p if fg(2) = 4. 

                                                                                    (3 marks)

Question 2 : Q2/D13/290420

The function g is defined by  g(x) = x + 3  and the  function f is such 

that fg(x) = x² + 6x + 7. 

Find,

a) the function f

b) the value of k for which  f(2k) = 8k + 30

                                                                                    (6 marks)

Answers T-QAD 28 April 2020

Check your answer and fill in the form to record your marks.

MyMarks 

Question 1

Marks for sketching : 
Construct table for x and f(x) for 0 till 6.             K1
Identify f(x) = 0 at x = 2.5                                    K1
Plot correctly all points                                        K1
Connect all points with straight line. V shaped   K1

Range of f(x)    :    0 ≤ f(x) ≤ 7                             N1


Question 2
a)

Marks for sketching : 

Construct table for x and f(x) for -1 till 5.             K1
plot correctly  and Identify f(x) = 0 at x = 2          K2
Connect all points with straight line. V shaped   K1

Draw g(x) correctly using any method                 K2

b)  0 ≤ x ≤ 3            N1

T-QAD Day 12 @ 28 April 2020

Notes Topic: Functions

Subtopic: Absolute value functions

Example:

Given the absolute value function f(x)= | x -  3| ,
a) Sketch the graph of f(x) for the domain of  – 1 ≤ x ≤ 4 and 
     state the corresponding range of values of f(x). 
b) find the values of x that have the image of 10.

Solution :

a) Prepare a table:  f(x)= | x -  3|
 
    For x = -1,     | -1 - 3 |  = | - 4 |
                                        =  4

x	-1	0	1	2	3	4
f(x)	4	3	2	1	0	1

   You must make sure your graph touch the x-axis. To calculate it: 

    The f(y) = 0 at x-axis. So, 

                             | x - 3| = 0, 

                               x - 3  = 0

                                    x  = 3.

 Then sketch the graph...

 The corresponding range of values of f(x) is  0 ≤ f(x) ≤ 4. 

 Notes : the range of values of f(x) is the range from the lowest value 

               of y to the highest value of y covered by the graph.

b) Since it is given that the image of f(x) =10,

     

          f(x)   =  10

     |x - 3|   =  10

so,    x - 3  = 10    or x - 3 = -10

              x   = 13              x = - 7.

T-QAD for TODAY

Question 1 : Q1/D12/280420

Sketch the graph of f(x) = | 2x -5 | for the domain 0 ≤ x ≤  6   and state the 

corresponding range of  f(x)                                                                                                                          

                                                                                              (5 marks)

Question 2 : Q2/D12/280420

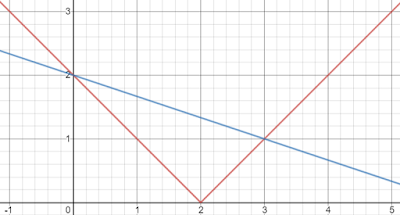
  The function of  f and g are defined by f(x) = | x - 2 |  and  g(x) = 2 - (x/3) respectively.

  a) On a piece of graph paper, draw the graph of y = f(x)      

       and y = g(x)  on the same axis  for - 1 ≤ x ≤  5

                                                                                                (6 marks)

  b) From your graphs, find the range of values of that satisfies the inequality 

       3 | 3 - 2 | ≤ 6 - x 

                                                                                                           (1 mark)

Answers T-QAD 27 April 2020

Check your answer and fill in the form to record your marks.

MyMarks 

T-QAD Day 11 @ 27 April 2020

Notes : Functions



A function is a special type of relation where each object in the domain has only one image in the codomain.

If a function maps x onto x² - 2, it is written using the function notation as

                    f : x à X² – 2 or f(x)= X² – 2

You can use Vertical Line Test to test whether the relation is a function.

If a vertical line crosses the relation on the graph only once in all locations, the relation is a function. However, if a vertical line crosses the relation more than once, the relation is not a function. Using the vertical line test, all lines except for vertical lines are functions

For further explanation.. You can watch this Video

          VIDEO 1

Example:

TQAD Today

Question 1 : Q1/D11/270420

                                                                                                        

Question 2 : Q2/D11/270420

                                                                                 

 Find :

a) the value of h and of k,                     (2 Marks)

b) the image of 10                                  (2 marks)

c) the object that has the image of -10    (2 marks)

d) the values of m, such that                                 

                 (2 marks)

                   

Answers T-QAD 26 April 2020

Check your answer and fill in the form to record your marks.

MyMarks 

Question 1:

a) { 1, 2, 3 , 4}              N1

b) { 1, 2, 3}                   N1

Question 2:

a) -3 and 3                       N1

b) many to one relation   N1

T-QAD Day 10 @ 26 April 2020

 Notes Topic: Functions

Subtopic: Relations


Module: FUNCTIONS click here to download.

Upload the module above. If you have printer, you can print it for your exercise. If not, just copy the question in your note book.
This week we will revise this chapter.

1. The relation between two sets can be represented by:

2. In relation between set (A) and set (B) :

Set (A) is known as domain. List of domain  { -2, 3, 4}

Set (B) is codomain. List of codomain {-4, 6, 8, 9}

 -2, 3, 4 are list of objects

 -4, 6, 8 are list of image

9 is non image because no object link to it.

All images are called RANGE.

3. Types of relations

Need further explanation? Please watch this video.

Video 1 

Example:

T-QAD for TODAY


Question 1 : Q1/D10/260420

The arrow diagram below shows the relation between set P and set Q. 

State

a) the codomain

b) the range

of the relation

                                                                                                         (2 marks)

Question 2 : Q2/D10/260420

The Cartesian graph below represents a relation from set P to set Q.

State

a) the objects of 9,

b) the type of the above relation.

                                                                                                         (2 marks)

                                                                                                      

Answers T-QAD 23 April 2020

Check your answer and fill in the form to record your marks.

MyMarks 

T-QAD Day 9 @ 23 April 2020

You may refer from previous notes.

Question 1 : Q1/D9/230420

        

Question 2 : Q2/D9/230420

Solve the equation   2 + log₃ (x – 1) = log₃ x           (3 marks)

Answers T-QAD 22 April 2020

Check your answer and fill in the form to record your marks.

MyMarks

 

Correction:

Final Answer for Q2,  x=2

T-QAD Day 8 @ 22 April 2020

Notes :Index Equations and Logarithmic equations

Question 1 : Q1/D8/220420

        (2 marks)                                                                                      

Question 2 : Q2/D8/220420

Solve the equation

Log_x 2 +log_x 4 – 2log_x 8 = – 3           (3 marks)

                                                                                                         

Answers T-QAD 21 April 2020

Check your answer and fill in the form to record your marks.
MyMarks 

T-QAD Day 7 @ 21 April 2020

Notes :Change of Base of Logarithms

Question 1 : Q1/D7/210420

If log_a 2 = h and log_a 3 = k, express log₆ 12 in terms of h and k.

                                                                                                         (3 marks)

Question 2 : Q2/D7/210420

Given that log_y 2 = k, find log₄ y in terms of k

                                                                                                         (4 marks)

Answers T-QAD 20 April 2020

Check your answer and fill in the form to record your marks.

MyMarks

T-QAD Day 6 @ 20 April 2020

Notes : Logarithms

·        Logarithm of a negative number is undefined

·        Logarithm of zero is also undefined

Example 1 :

Example 2 :

Solution : 

Question 1 : Q1/D6/200420

                                                                                                         (2 marks)

Question 2 : Q2/D6/200420

                                                                                                         (3 marks)

Answers T-QAD 19 April 2020

Check your answer and fill in the form to record your marks.
MyMarks 

Question 1:

Question 2 :